[DL] Data Augmentation

PV:

Introduction

众所周知，Deep Learning现如今的繁荣，和大数据、GPU和深度学习算法都是离不开关系的。Deep Learning模型参数众多，需要海量的数据进行拟合，否则很容易overfitting到training set上。而现实情况下，我们不一定能很容易地获取大量高质量标注样本，因此，Data Augmentation则起到了非常大的作用了。这便是本文所要讲述的主角。

Mixup

Paper: mixup: Beyond Empirical Risk Minimization

Mixup的核心idea如下：
$$
\tilde{x}=\lambda x_i + (1-\lambda) x_j
$$

$$
\tilde{y}=\lambda y_i + (1-\lambda) y_j
$$
其中，$x_i, x_j$为raw input vectors，$y_i, y_j$为one-hot encodings。

Mixup extends the training distribution by incorporating the prior knowledge that linear interpolations of feature vectors should lead to linear interpolations of the associated targets.

Mixup的PyTorch代码如下，是不是非常简洁？

1
2
3
4
5
6
7
8
# y1, y2 should be one-hot vectors
for (x1, y1), (x2, y2) in zip(loader1, loader2):
    lam = numpy.random.beta(alpha, alpha)
    x = Variable(lam * x1 + (1. - lam) * x2)
    y = Variable(lam * y1 + (1. - lam) * y2)
    optimizer.zero_grad()
    loss(net(x), y).backward()
    optimizer.step()

What is mixup doing?

The mixup vicinal distribution can be understood as a form of data augmentation that encourages the model $f$ to behave linearly in-between training examples. We argue that this linear behaviour reduces the amount of undesirable oscillations when predicting outside the training examples. Also, linearity is a good inductive bias from the perspective of Occam’s razor, since it is one of the simplest possible behaviors.

mixup is a data augmentation method that consists of only two parts: random convex combination of raw inputs, and correspondingly, convex combination of one-hot label encodings.

Hide-and-Seek

Paper: Hide-and-seek: Forcing a network to be meticulous for weakly-supervised object and action localization

Hide-and-Seek (HaS)可视为一种提高localisation任务的data augmentation方法，其核心思想也非常简单，即在训练阶段，将input image先划分成$S\times S$个grid，然后随机以概率$p$hidden掉一些grid，来消除DCNN仅仅对image中最discriminative parts的强依赖，而是对relevent parts都产生一定的response，从而提高模型在预测阶段的robustness。

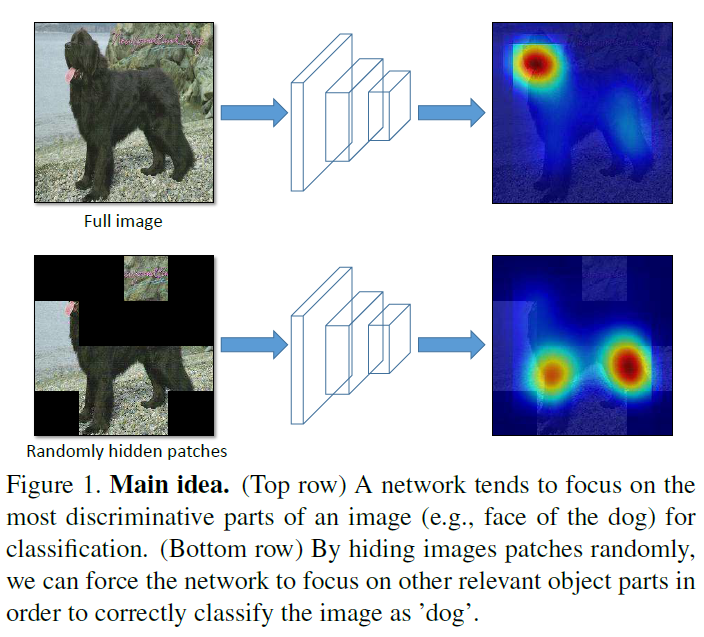
Main Idea of HaS

已上图为例，若该image中最discriminative part是dog face，我们在训练阶段从input image中random drop的时候将dog face hidden掉了，那么这样就会迫使模型去寻找其他relevent parts (例如tail和leg)来辅助学习。通过在每个training epoch中随机hidden different parts，模型接受了image不同的parts作为输入，来使得模型关注不同的relevent parts，而不是最discriminative part。

Delving Into HaS

Hiding random image patches

通过randomly hide patches，我们可以保证input image中最discriminative的part并非总是可以被模型get到，既然模型没法总是get到最discriminative的part，那么它自然就会从其他relevent but not that discriminative part中进行学习，从而解决了模型对discriminative part强依赖的缺陷。

具体来讲，是这样的：给定一张size为 $W\times H\times 3$的 training image $I$，我们首先将其划分为固定size的patches ($S\times S$)，然后就得到了一共$(W\times H)/(S\times S)$个patches，然后以概率$p_{hide}$进行patch hiding操作。这样我们就得到了new image $I^{‘}$，来作为classification CNN的输入。在test阶段，将整张图作为输入(不做任何hiding)。

HaS Overview

Setting the hidden pixel values

因为training阶段做了patch hiding而test阶段没有，这就存在discrepancy。这就会导致training阶段和test阶段的第一个conv layer activation有不同的distribution。而一个trained network要拥有良好的泛化能力，activiation的distribution应该是大致一样的。也就是说，对于DNN中连接到$x$ units的$w$ weights，$w^Tx$的distribution在training/test阶段应该大致相同。然而，在我们的设定中，因一些patch被hidden，而另一些没有被hidden，因此就不能保证activation distribution大致相同了。

假设size为$K\times K$的conv kernel $F$，对应3-dimensional weights $W=\{w_1,\cdots,w_{k\times k}\}$，应用到一个RGB patch $X=\{x_1,\cdots,x_{k\times k}\}$上。另$v$代表每一个hidden pixel的RGB value。我们可以得到3种activation:

  1. $F$完全在visible patch中，得到输出$\sum_{i=1}^{k\times k} w_i^T x_i$。
  2. $F$完全在hidden patch中，得到输出$\sum_{i=1}^{k\times k}w_i^T v$。
  3. $F$部分位于visible patch，部分位于hidden patch，得到输出$\sum_{m\in visible}w_m^Tx_m + \sum_{n\in hidden}w_n^T v$。

在test阶段，$F$总会位于visible patch中(因为HaS只在training阶段work)，因此会输出$\sum_{i=1}^{k\times k}w_i^T x_i$。这种输出仅仅会match到我们上面提到的第一种情况(即$F$完全在visible patch中)。对于后面两种情况，training阶段的activation和test阶段的activation也还是不同。

我们通过将hidden pixel的RGB value设置为整个数据集上图片的mean RGB vector $v=\mu=\frac{1}{N_{pixels}}\sum_j x_j$来解决以上问题。
其中，$N_{pixels}$代表数据集上的所有像素。

我们不妨来分析一下为什么这能work？
根据期望，一个patch的输出和averaged-valued patch的输出应该是一样的：$\mathbb{E}[\sum_{i=1}^{k\times k}w_i^Tx_i]=\sum_{i=1}^{k\times k}w_i^T\mu$。若将$v$换成$\mu$，那么上面提到的第2种和第3种情况的输出都会是$\sum_{i=1}^{k\times k}w_i^T \mu$，然后就会和test阶段的expected output能match上。

文中用到的检测算法属于weakly-supervised detector (即仅仅给定image的category annotation，不给bbox)，因此整体framework是基于CAM的，不熟悉的读者可以去阅读CAM的原文。

Analysis

  • With dropout: 因dropout随机drop掉了RGB channel pixels，image中最discriminative的information依然可以以很高的可能性被模型get到，因此还是会促使模型更多地关注最discriminative的部分。
  • GAP VS GMP: 因为GAP促使模型关注所有的discriminative parts，而GMP只关注最discriminative part。那是否GMP无用呢？实验证明，接入了HaS后的GMP带来了很大的提升，这种improvement可以归因于max pooling对noise更robust。

SamplePairing

Paper: Data Augmentation by Pairing Samples for Images Classification

SamplePairing是Deep Learning领域一篇非常非常简单的paper，简单到几乎小学生都可以看懂。思想和前面的Mixup有点像，但是却更简单，而且数学解释也不如Mixup做得好。
这里就大致讲一下SamplePairing的idea吧：
挑选training set中（注：当然也可以从非training set中挑选，但作者做了实验发现从training set中选取的能取得更好的效果）图像$I$与图像$J$，然后合成新样本$I^{‘}=0.5I + 0.5J$，其中新样本$I^{‘}$的label与图像$I$保持一致，这样就可以从$N$个样本中合成$N^2$个样本。如下图所示：

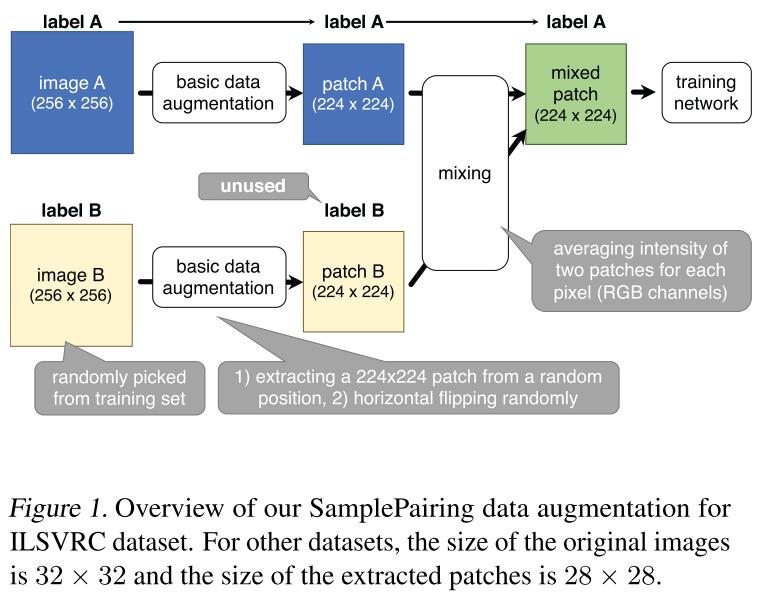
Sample Pairing

对于算法细节就不多说了，因为实在是太简单。下面介绍一下paper中值得注意的点吧：

  1. SamplePairing在100分类任务上的效果比1000分类任务上的效果更好。
  2. SamplePairing增大了training loss，但是却降低了validation loss（很好理解，mix了两个不同label的samples之后，模型在training set上肯定拟合的不如原来好）。
  3. 关于样本$I$与样本$J$的选择问题：随机从所有category中挑选能取得最好的效果。
  4. 关于样本$I$与样本$J$的权重设置问题：设置0.5（即equal intensity mix）效果最好。
  5. 很适合医学图像分析这类样本非常少的分类场景中。

RandomErasing

Paper: Random erasing data augmentation
Code: RandomErasing.PyTorch

这篇也是非常非常简单的paper，核心idea就是在训练过程中挑选图像中一块连续的区域，然后填充随机数值，来使得模型对occlusion更鲁棒。与常见的data augmentation操作Random Crop有以下不同：

  1. 图像中的object只有一部分被occlude，而overall structure信息是完整的
  2. erased region被随机填充数值，可视为在图片中添加了noise

算法细节如下图所示，因为太简单就不细说了：
Random Erasing

此外，作者在实验中还发现：

  1. RandomErasing和Random Flipping/Random Crop可以起到complementary的效果，因此可以放心地一起用。
  2. 填充值为Random Number时能取得最佳效果。

Cutout

Paper: Improved regularization of convolutional neural networks with cutout

又是一篇非常简单的paper，即在input image中随机mask掉一块连续区域来使得模型更好地利用full context image information，而非仅仅那么一小块的specific visual features，思想和Random Erasing其实非常相似。

Dropout被广泛应用于DNN（主要是FC layer和MLP）的regularization中，但是在conv layer却并没有MLP中那么有效，原因主要如下：

  1. conv layer因parameter sharing机制，参数本来就已经比FC layer少了很多，因此overfitting现象自然比FC layer轻。
  2. 图像中neighboring pixel共享相同的信息，因此若其中某些pixel被drop掉，那么下一层网络依然可以从neighbor pixel获取相似的信息。

因此，Dropout在conv layer中仅仅起到增强对noisy inputs鲁棒性的作用，而非起到像FC layer中的model averaging effect。

Mask image pixel的方式如下：

  1. 在每一次epoch中，提取并存储每张图maximally activated feature map
  2. 在下一个epoch中，upsample上一步存储的feature map到input resolution，再利用feature map的均值来作为mask

此外，作者还发现：

  1. mask掉的区域不能太大
  2. 随着category数量的增加，最佳的cutout size逐步变小，原因可能是细粒度分类中context信息并不如object的细节重要

Reference

  1. Zhang, Hongyi, et al. “mixup: Beyond empirical risk minimization.” International Conference on Learning Representations (2018).
  2. Kumar Singh, Krishna, and Yong Jae Lee. “Hide-and-seek: Forcing a network to be meticulous for weakly-supervised object and action localization.” Proceedings of the IEEE International Conference on Computer Vision. 2017.
  3. Inoue, Hiroshi. “Data augmentation by pairing samples for images classification.” arXiv preprint arXiv:1801.02929 (2018).
  4. Zhong Z, Zheng L, Kang G, et al. Random erasing data augmentation[J]. arXiv preprint arXiv:1708.04896, 2017.
  5. DeVries T, Taylor G W. Improved regularization of convolutional neural networks with cutout[J]. arXiv preprint arXiv:1708.04552, 2017.
  6. Yun S, Han D, Oh S J, et al. Cutmix: Regularization strategy to train strong classifiers with localizable features[C]. ICCV, 2019.

Powered by Hexo and Hexo-theme-hiker

Copyright © 2018 - 2023 LucasX All Rights Reserved.

UV : | PV :