[ML] Semi-supervised & Unsupervised Learning

Introduction

Semi-supervised Learning和Unsupervised Learning是ML research领域一个非常活跃、也非常值得探索的方向，为什么这么说呢？现如今应用最广泛的ML算法叫作Deep Learning，而熟悉Deep Learning的同学都知道，这类算法实际上是非常“蠢”的，即要用大量标记样本去train一个DNN，来学习某种mapping function $\mathcal{f}(x)=y$，而人类在认识某样物品时，可是不需要用这么多带标记样本去train的。如果能在Semi-supervised Learning和Unsupervised Learning取得和Supervised Learning一样的精度，那我们就可以不需要雇人打标签了。本文旨在记录一下近些年来ML/DL/CV等领域个人认为一些比较insightful的paper。

注：如果读者身处工业界，可能最有效的方法还是堆数据，本文更偏research一点。

Learning by Association

Paper: Learning by Association–A versatile semi-supervised training method for neural networks

这是一篇发表在CVPR’2017上的paper，作者介绍了一种semi-supervised learning方法，并且在MNIST、SHVN以及Transfer Learning实验中均取得了非常好的效果。idea大体上也比较简单，说来惭愧，笔者当时刚接触DL时，也有过和本文非常相似的idea，无奈没有做出来。

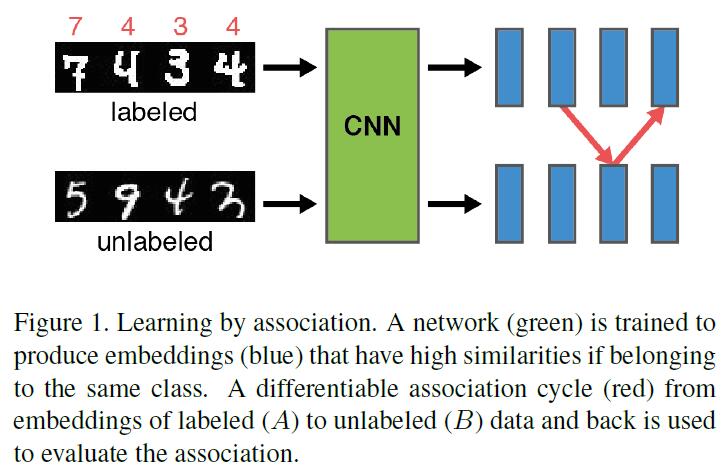
作者提出了一种ML方法，称之为Learning by Association，所谓Association就是指从labeled samples到unlabeled samples，然后在返回到labeled samples的embedding，读者可能就会问，那你怎么确定从labeled samples walk 到 unlabeled samples的时候，unlabeled samples的category是和labeled sample的category相匹配的呢？因此，直白点描述呢，该算法的优化目标就是encourage 这种正确的association，并且惩罚不正确的association。

We propose a novel training method that follows an intuitive approach: learning by association (Figure 1). We feed a batch of labeled and a batch of unlabeled data through a network, producing embeddings for both batches. Then, an imaginary walker is sent from samples in the labeled batch to samples in the unlabeled batch. The transition follows a probability distribution obtained from the similarity of the respective embeddings which we refer to as an association. In order to evaluate whether the association makes sense, a second step is taken back to the labeled batch - again guided by the similarity between the embeddings. It is now easy to check if the cycle ended at the same class from which it was started. We want to maximize the probability of consistent cycles, i.e., walks that return to the same class. Hence, the network is trained to produce embeddings that capture the essence of the different classes, leveraging unlabeled data. In addition, a classification loss can be specified, encouraging embeddings to generalize to the actual target task.

Purely Unsupervised Learning

本文主角Learning by Association是Semi-supervised Learning，先来介绍一下Unsupervised Learning的特点，Unsupervised Learning的有效性依赖于合适的cost function与balanced datasets。对于分类任务而言，invariance to this very phenomenon might be more preferable.

Delve into Learning by association

Learning by Association算法work的一个assumption就是若unlabeled sample batch和labeled sample batch属于同一类，那么一个良好的embedding应该具备非常高的Similarity。令$A_{img}$代表labeled images batch，$B_{img}$代表unlabeled images batch，DNN输出embedding vectors A 和 B，然后walker从根据其mutual similarity从A走到B，并且再从B返回到A，若该walker返回到了与其出发相同的class，则说明walk过程正确。

数学上的problem formulation就是这样的：Learning by Association的目标就是最大化$A\to B\to A$正确的walk。A 和 B 是matrices，它的row代表batch中samples的索引，embedding A 和 B 的相似度定义为：
$$
M_{ij}:=A_i\cdot B_j
$$

然后通过softmax $M$ 将这些 similarities 转换到从 $A$ 到 $B$ 的 transition probabilities：
$$
P_{ij}^{ab}=P(B_j|A_i):=(softmax_{cols}(M))_{ij}=exp(M_{ij})/\sum_{j^{‘}}exp(M_{ij^{‘}})
$$

同样地，从 $B$ 再返回到 $A$ 的transition probability $P^{ba}$ 可以表示为：
$$
P_{ij}^{aba}:=(P^{ab}P^{ba})_{ij}=\sum_k P_{ik}^{ab} P_{kj}^{ba}
$$

correct walk的probability为：
$$
P(correct_{walk})=\frac{1}{|A|}\sum_{i\sim j} P_{ij}^{aba}
$$
$i\sim j$ 即 $class(A_i)=class(A_j)$。

最终的 Loss 即为多个joint loss combination：
$$
\mathcal{L}_{total}=\mathcal{L}_{walker}+\mathcal{L}_{visit}+\mathcal{L}_{classification}
$$

• Walker Loss: The goal of our association cycles is consistency. A walk is consistent when it ends at a sample with the same class as the starting sample. This loss penalizes incorrect walks and encourages a uniform probability distribution of walks to the correct class. The uniform distribution models the idea that it is permitted to end the walk at a different sample than the starting one, as long as both belong to the same class. The walker loss is defined as the cross-entropy $H$ between the uniform target distribution of correct round-trips $T$ and the round-trip probabilities $P^{aba}$.
  $$
  \mathcal{L}_{walker}:=H(T,P^{aba})
  $$

with the uniform target distribution
$$
T_{ij}=
\begin{cases}
1/|class(A_i)| & class(A_i)=class(A_j) \\
0 & else \\
\end{cases}
$$
where $|class(A_i)|$ is the number of occurrences of $class(A_i)$ in $A$.

• Visit loss. There might be samples in the unlabeled batch that are difficult, such as a badly drawn digit in MNIST. In order to make best use of all unlabeled samples, it should be beneficial to “visit” all of them, rather than just making associations among “easy” samples. This encourages embeddings that generalize better. The visit loss is defined as the cross-entropy $H$ between the uniform target distribution $V$ and the visit probabilities $P^{visit}$. If the unsupervised batch contains many classes that are not present in the supervised one, this regularization can be detrimental and needs to be weighted accordingly.
  $$
  \mathcal{L}_{visit}:=H(V,P^{visit})
  $$
  where the visit probability for examples in $B$ and the uniform target distribution are defined as follows:
  $$
  P_{j}^{visit}:=<P_{ij}^{ab}>_i
  $$

$$
V_j:=1/|B|
$$

• Classification loss. So far, only the creation of embeddings has been addressed. These embeddings can easily be mapped to classes by adding an additional fully connected layer with softmax and a cross-entropy loss on top of the network. We call this loss classification loss. This mapping to classes is necessary to evaluate a network’s performance on a test set. However, convergence can also be reached without it.

Analysis

• In all other scenarios with a greater number of labeled samples, the general pattern we observed is that performance improves with greater amounts of unlabeled data. This indicates that it is indeed possible to boost a network’s performance just by adding unlabeled data using the proposed associative learning scheme.
• A particular case occurs when all data is used in the labeled batch (last row in Table 3): Here, all samples in the unlabeled set are also in the labeled set. This means that the unlabeled set does not contain new information. Nevertheless, employing associative learning with unlabeled data improves the network’s performance. $\mathcal{L}_{walker}$ and $\mathcal{L}_{visit}$ act as a beneficial regularizer that enforces similarity of embeddings belonging to the same class. This means that associative learning can also help in situations where a purely supervised training scheme has been used, without the need for additional unlabeled data.
• If the visit loss weight is too high, the effect seems to be over regularization of the network. This suggests that the visit loss weight needs to be adapted according to the variance within a data set. If the distributions of samples in the (finitely sized) labeled and unlabeled batches are less similar, the visit loss weight should be lower.

Reference

1. Haeusser, Philip, Alexander Mordvintsev, and Daniel Cremers. “Learning by Association–A Versatile Semi-Supervised Training Method for Neural Networks.” Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2017.