[DL] Siamese Neural Network

Introduction

Siamese Network也是一个比较有意思的网络结构，并且在许多领域都有了非常成功的应用，本文主要记录这些具体的application中一些代表性的paper。

@LucasXU注：对网络结构感兴趣的可以阅读我的另外一篇文章Architecture。

Siamese Network

Paper: Signature verification using a “siamese” time delay neural network

这算是Siamese Network最早的一篇文章了，记录了用Siamese Network做signature verification的应用。整体上比较简单，就记录一下key points吧。

• 本文中用到的Siamese Network是两个identical subnetwork，来从两张input image中提取feature，那么verification就是比较extracted feature和该signer之前保存的signature的feature vector之间的distance。

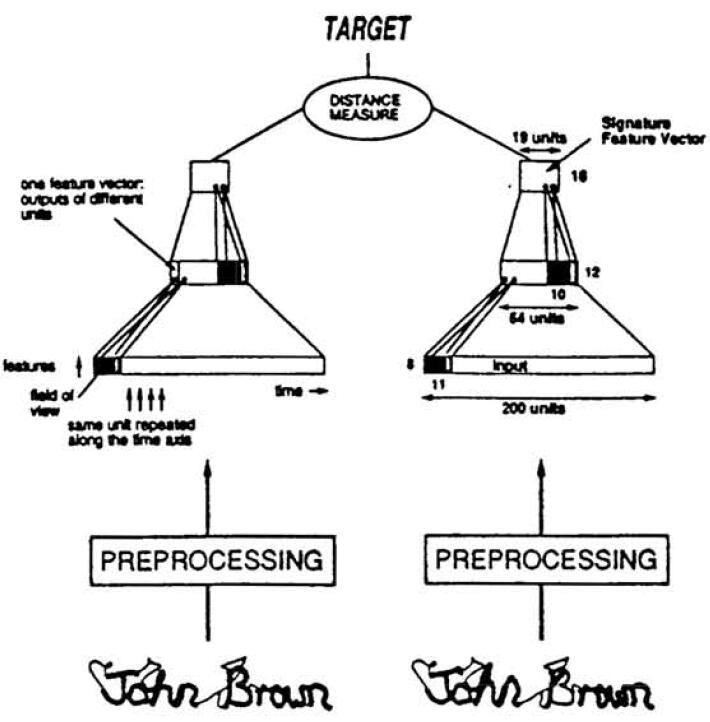
• 网络中所有的weights都是learnable，但是两个subnetwork被限制于weights都是相同的。
• 在Testing的时候，只用到其中一个subnetwork的输出作为feature vector，来和stored signature feature vector进行比对distance。

Siamese neural networks for One-shot Image Recognition

Paper: Siamese neural networks for one-shot image recognition

这是一篇发表在ICML’15上的Paper，主要讲的是用Siamese Network做one-shot learning，在讲解这篇paper之前，先来介绍几个概念吧。

• One-shot Learning: 在多分类问题中，对于每一个类，我们只观察一个sample。
• Zero-shot Learning: 任何一个sample都不能给模型观测。

Deep Siamese Networks for Image Verification

先上基础的Siamese Network的网络结构，大致是这样的：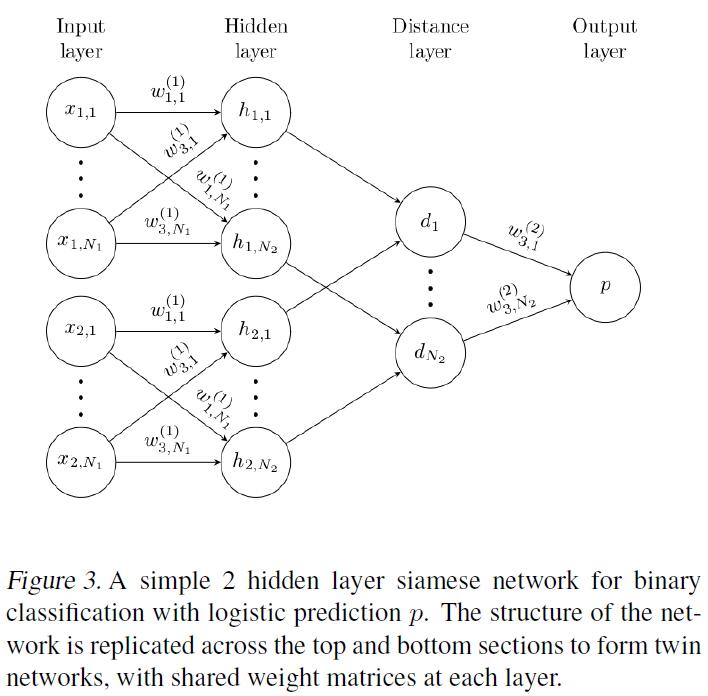

本文采用twin feature $h_1$与$h_2$之间加权的$L_1$ distance，并结合sigmoid map到$[0, 1]$区间，来作为metric。

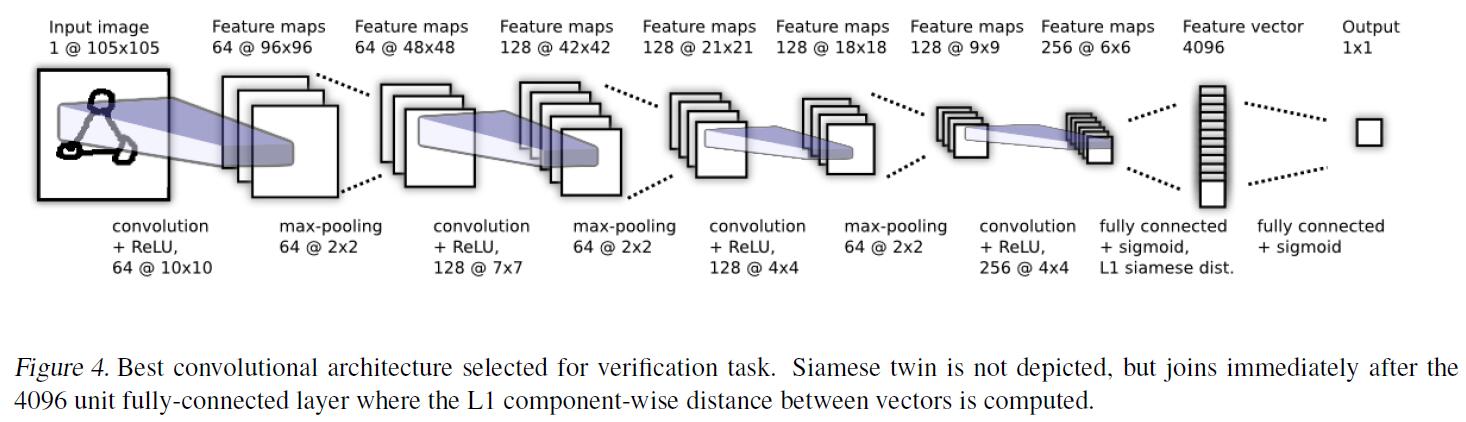
上述是本文用到的Convolutional Siamese Architecture，最后一个conv layer的feature map被flatten成feature vector，然后紧跟另一个layer用来计算每个siamese twin的induced distance，再作为sigmoid function的输入。即：
$$
p=\sigma(\sum_j \alpha_j |h_{1,L-1}^{(j)} - h_{2,L-1}^{(j)}|)
$$
$\alpha_j$是衡量component-wise distance的权重，通过training过程中自动学习。网络的最后一层向$(L-1)$-th hidden layer的learned feature space引入了一种metric来衡量feature vector的similarity。

Loss Function

设$M$为mini-batch size，$i$代表第$i$个batch。令$y(x_1^{(i)}, x_2^{(i)})$为M-dimensional feature vector。若$x_1$和$x_2$为相同class，则$y(x_1^{(i)}, x_2^{(i)})=1$；反之$y(x_1^{(i)}, x_2^{(i)})=0$。采用Cross Entropy作为loss：
$$
\mathcal{L}(x_1^{(i)}, x_2^{(i)})=y(x_1^{(i)}, x_2^{(i)})log p(x_1^{(i)}, x_2^{(i)}) + (1- y(x_1^{(i)}, x_2^{(i)}))log (1-p(x_1^{(i)}, x_2^{(i)})) + \lambda^T |w|^2
$$

One-shot Learning

当网络训练完成，就可以用one-shot learning来测试learned feature的generalization ability。

Suppose we are given a test image $x$, some column vector which we wish to classify into one of $C$ categories. We are also given some other images $\{x_c\}_{c=1}^C$, a set of column vectors representing examples of each of those $C$ categories. We can now query the network using $x$, $x_c$ as our input for a range of $c=1,\cdots,C^2$. Then predict the class corresponding to the maximum similarity.

$$
C^{\star}=\mathop{argmax} \limits_{c} p^{(c)}
$$

Siamese Network in Visual Tracking

Paper: Learning by tracking: Siamese cnn for robust target association

这是一篇利用Siamese Network做tracking的paper，由于关注点并非visual tracking，所以这里只记录Siamese Network的设计和使用部分。

本文用到的tracking framework主要idea如下：

• 利用CNN学习local-spatio-temporal features
• 学习contextual features来encode position variants
• XGBoost来对combined features(local + contextual)进行classification

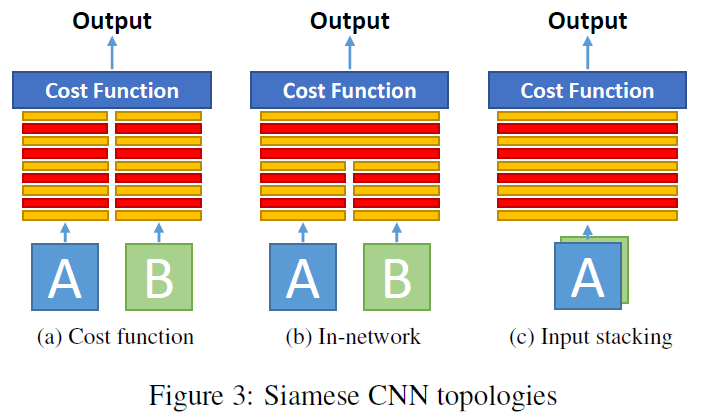
涉及到matching问题，一个很自然的idea就是使用Siamese Network + Contrastive Loss。Siamese Network的组合方式有如下3种：

• Cost Function: Input patches are processed by two parallel branches featuring the same network structure and weights. Finally, the top layers of each branch are fed to a cost function [12, 49] that aims at learning a manifold where different classes are easily separable.
• In-Network: The top layers of the parallel branches processing the two different inputs are concatenated and some more layers are added on top of that [21, 62]. Finally, the standard softmax log-loss function is employed.
• Joint data input: The two input patches are stacked together forming a unified input to the CNN [21]. Again, the softmax log-loss function is used here.

网络结构是这样的：

Input接受4种类型的information，即待比对的patch(normalized LUV color space) $I_1$和$I_2$，对应的optical flow components $O_1$和$O_2$。

• Loss of Siamese Network:
  $E=\frac{1}{2N}\sum_{n=1}^N (y)d + (1-y)max(\tau - d,0)$
  其中，$d=|a_n-b_n|_2^2$代表$twin-subnetwork$顶层FC layer输出 $a_n$和$b_n$的$L_2$ normalized response。
• CNN的结构：先走conv layer with PreReLU $C_{1,2,3}$；然后是max-pooling layer来使得网络对miss alignment更加robust；然后是fully-connected layers $F_{4,5,6,7}$来capture图片中distant parts features的correlation、以及cross-modal的dependencies；最后一个FC layer的输出进入到binary softmax layer，来产生class label (match/no match)的distribution。$F_6$的输出被用作raw patch matching的feature vector。
• Data augmentation: geometric distortion (rotation, translation, skewing, scaling, flipping); image distortion (guassian blur, noise, gamma).

Reference

1. Bromley, Jane, et al. “Signature verification using a” siamese” time delay neural network.” Advances in neural information processing systems. 1994.
2. Koch, Gregory, Richard Zemel, and Ruslan Salakhutdinov. “Siamese neural networks for one-shot image recognition.” ICML Deep Learning Workshop. Vol. 2. 2015.
3. Leal-Taixé, Laura, Cristian Canton-Ferrer, and Konrad Schindler. “Learning by tracking: Siamese cnn for robust target association.” Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops. 2016.
4. Siamese Networks: Algorithm, Applications And PyTorch Implementation