Introduction
Regularization是Machine Learning中一个非常重要的概念,是对抗Overfitting最有用的利器。DNN由于参数众多,很容易overfitting,若直接选用small model,则会导致model特征学习、分类能力不足。因此现实中往往是 使用较大的模型 + 正则化 来解决相应问题。因此本文简要介绍一下Deep Learning中常用的正则化方法。
$$
\tilde{J}(\theta;X,y)=J(\theta;X,y)+\alpha\Omega(\theta)
$$
参数范数惩罚
我们通常只对weight做惩罚,而不对bias做正则惩罚。精确拟合bias所需的数据通常比拟合weight少得多,每个weight会指定两个变量如何相互作用。而每个bias仅控制一个单变量。这意味着我们不对其进行正则化也不会导致太大的方差。
在DNN中,有时会希望对Network的每一层使用单独的惩罚,并分配不同的$\alpha$系数,而寻找合适的多个超参代价很大。因此为了减少搜索空间,我们会在所有层使用相同的weight decay。
$L_2$ Regularization
为简单起见,假定DNN中没有bias,因此$\theta$就是$w$。模型Loss Function如下:
$$
\tilde{J}(w;X,y)=\frac{\alpha}{2}w^Tw+J(w;X,y)
$$
与之对应的梯度为:
$$
\bigtriangledown_w \tilde{J}(w;X,y)=\alpha w+\bigtriangledown_w J(w;X,y)
$$
使用SGD更新权重:
$$
w\leftarrow w-\epsilon(\alpha w+\bigtriangledown_w J(w;X,y))
$$
换种写法就是:
$$
w\leftarrow (1-\epsilon\alpha)w-\epsilon\bigtriangledown_w J(w;X,y)
$$
可以看到,加入weight decay后会引起学习规则的修改,即在每一步执行通常的SGD之前会 先收缩权重向量(将权重向量乘以一个常数因子)。
以Linear Regression为例,其Cost Function是MSE:
$$
(Xw-y)^T(Xw-y)
$$
我们添加$L_2$ Regularization之后,Cost Function变为:
$$
(Xw-y)^T(Xw-y)+\frac{1}{2}\alpha w^Tw
$$
这将正规方程的解由 $w=(X^TX)^{-1}X^Ty$ 变为 $w=(X^TX+\alpha I)^{-1}X^Ty$。其中,矩阵$X^TX$与协方差矩阵$\frac{1}{m}X^TX$成正比。$L_2$ Regularization将这个矩阵替换为上式中的$(X^TX+\alpha I)^{-1}$,这个新矩阵与原来的是一样的,不同的仅仅是在对角线加了$\alpha$。这个矩阵的对角项对应每个输入特征的方差。我们可以看到,$L_2$ Regularization能让学习算法“感知到”具有较高方差的输入$x$,因此与输出目标的协方差较小(相对增加方差)的特征的权重将会收缩。
$L_1$ Regularization
为简单起见,假定DNN中没有bias,因此$\theta$就是$w$。模型Loss Function如下:
$$
\tilde{J}(w;X,y)=\alpha||w||_1+J(w;X,y)
$$
对应的梯度:
$$
\bigtriangledown_w \tilde{J}(w;X,y)=\alpha sign(w)+\bigtriangledown_w J(w;X,y)
$$
可与看到,此时正则化对梯度的影响不再是线性地缩放每个$w_i$,而是添加了一项与$sign(w_i)$同号的常数,使用这种形式的梯度之后,我们不一定能得到$J(X,y;w)$二次近似的直接算数解($L_2$正则化时可以)。
我们可以将$L_1$ Regularization Cost Function的二次近似分解成关于参数的求和:
$$
\hat{J}(w;X,y)=J(w^{\star};X,y)+\sum_i [\frac{1}{2}H_{i,i}(w_i-w_i^{\star})^2+\alpha |w_i|]
$$
如下形式的解析解(对每一维$i$)可以最小化这个近似Cost Function:
$$
w_i=sign(w_i^{\star})max\{|w_i^{\star}|-\frac{\alpha}{H_{i,i}},0\}
$$
此时:
1) 若$w_i^{\star}\leq \frac{\alpha}{H_{i,i}}$,正则化后目标中的$w_i$最优值是0。这是因为在方向$i$上$J(w;X,y)$对$\hat{J}(w;X,y)$的贡献被抵消,$L_1$ Regularization将$w_i$推至0。
2) 若$w_i^{\star}> \frac{\alpha}{H_{i,i}}$,正则化不会将$w_i$的最优值推至0,而仅仅在那个方向上移动$\frac{\alpha}{H_{i,i}}$的距离。
相比$L_2$ Regularization,$L_1$ Regularization会产生更稀疏的解(最优值中的一些参数为0)。
作为约束的范数惩罚
$$
\theta^{\star}=\mathop{argmin} \limits_{\theta} \mathcal{L}(\theta,\alpha^{\star})=\mathop{argmin} \limits_{\theta} J(\theta;X,y)+\alpha^{\star}\Omega(\theta)
$$
如果$\Omega$是$L_2$范数,那么权重就是被约束在一个$L_2$球中;如果$\Omega$是$L_1$范数,那么权重就是被约束在一个$L_1$范数限制的区域中。
Data Augmentation
在NN的输入层注入噪声也可以看作Data Augmentation的一种方式。然而,NN对噪声不是很robust。改善NN robustness的方法之一是简单地将随机噪声添加到输入再训练。输入噪声注入是一些Unsupervised Learning Algorithm的一部分(例如Denoise Auto Encoder)。向hidden layer施加噪声也是可行的,这可以被看作在多个抽象层上进行的Data Augmentation。
Robustness of Noise
对某些模型而言,向输入添加方差极小的噪声等价于对权重施加范数惩罚。一般情况下,注入噪声远比简单地收缩参数强大,特别是噪声被添加到hidden units时会更加强大。
Multi-Task Learning
MTL是通过合并几个任务中的样例(可以视为对参数施加的软约束)来提高泛化的一种方式。当模型的一部分被多个额外的任务共享时,这部分将被约束为良好的值,通常会带来更好的泛化能力。
Early Stopping
在训练中只返回使validation set error最低的参数设置,就可以获得使validation set更低的模型(并且因此有希望获得更好的test set error)。在每次validation set有所改善后,我们存储模型参数的副本。当训练算法终止时,我们返回这些参数而不是最新的参数。当validation set error在事先指定的循环次数内没有进一步改善时,算法就会终止。这种策略称为Early Stopping。
对于weight decay,必须小心不能使用太多的weight decay,以防止网络陷入不良局部极小点。
Early Stopping需要validation set,这意味着某些training samples不能被输入到模型。为了更好地利用这一额外数据,我们可以在完成Early Stopping的首次训练之后,进行额外的训练。在第二轮,即额外的训练步骤中,所有的training data都会被包括在内。
- 一种策略是再次初始化模型,然后使用所有数据再次训练。在第二轮训练过程中,我们使用第一轮Early Stopping确定的 最佳Epoch。
- 另一种策略是保持从第一轮训练获得的参数,然后使用全部数据继续训练。在这个阶段,已经没有validation set指导我们需要训练多少步停止。我们可以监控validation set的平均loss,并继续训练,直到它低于Early Stopping终止时的目标值。

为什么Early Stopping具有Regularization效果?
Bishop 认为Early Stopping可以将优化过程的参数空间限制在初始参数值$\theta_0$的小领域内。事实上,在二次误差的简单Linear Model和Gradient Descend情况下,我们可以展示Early Stopping相当于$L_2$ Regularization。
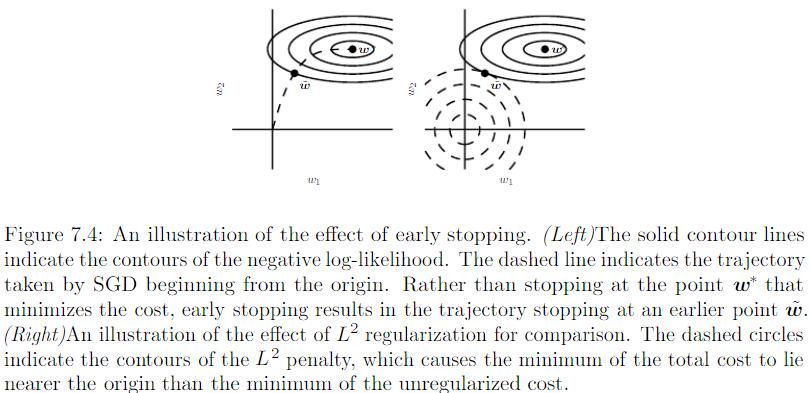
参数绑定和参数共享
假设有两个model执行两个分类任务,但输入分布稍有不同。这两个模型将输入映射到两个不同但相关的输出:$\hat{y}^{(A)}=f(w^{(A)},x)$和$\hat{y}^{(B)}=f(w^{(B)},x)$。
我们可以想象,这些任务会足够相似,因此我们认为模型参数应彼此接近:$\forall_i,w_i^{(A)}$应该与$w_i^{(B)}$接近,我们可通过正则化利用此信息,即:$\Omega(w^{(A)},w^{(B)})=||w^{(A)}-w^{(B)}||_2^2$。这里使用$L_2$ Regularization,也可以使用其他Regularization。
正则化一个模型(监督模式下训练的分类器)的参数,使其接近另一个无监督模式下训练的模型参数,构造的这种架构使得分类模型中的许多参数能与无监督模型中对应的参数匹配。
CNN通过在多个位置共享参数来考虑 平移不变性。相同的特征(具有相同权重的hidden units)在输入的不同位置上计算获得,这意味着无论人脸在图像中的第$i$列或是$i+1$列,我们都可以使用相同的feature detector找到人脸。
Sparse Representation
Weight decay是直接惩罚模型参数,另一种策略是惩罚NN中的激活单元,稀疏化激活单元。这种策略间接地对模型参数施加了复杂惩罚。
表示的稀疏惩罚正则化是通过向Loss Function $J$ 添加对表示的范数惩罚来实现的,记作$\Omega(h)$:
$$
\tilde{J}(\theta;X,y)=J(\theta;X,y)+\alpha\Omega(h)
$$
对表示元素的$L_1$惩罚诱导稀疏的表示:$\Omega(h)=||h||_1=\sum_i|h_i|$。
还有一些其他方法通过激活值的硬性约束来获得表示稀疏,例如正交匹配跟踪通过解决以下约束优化问题将输入值$x$编码成表示$h$:
$$
\mathop{argmin} \limits_{h,||h||_0< k} ||x-Wh||^2
$$
其中$||h||_0$是$h$中非零项的个数。当$W$被约束为正交时,我们可以高效地解决这个问题。
Bagging和其他集成方法
Why Model Averaging Works?
假设我们有$k$个regression model,每个model在每个例子上的误差是$\epsilon_i$,这个误差服从零均值方差为$\mathbb{E}[\epsilon_i^2]=v$且协方差为$\mathbb{E}[\epsilon_i\epsilon_j]=c$的多维正态分布。通过所有集成模型的平均预测所得误差是$\frac{1}{k}\sum_i\epsilon_i$。集成模型的MSE期望是:
$$
\mathbb{E}[(\frac{1}{k}\sum_i \epsilon_i)^2]=\frac{1}{k^2}\mathbb{E}[\sum_i (\epsilon_i^2+\sum_{j\neq i}\epsilon_i \epsilon_j)]=\frac{v}{k}+\frac{k-1}{k}c
$$
在误差完全相关即$c=v$的情况下,MSE减少到$v$,所以模型平均没有任何帮助。在错误完全不相关即$c=0$的情况下,该集成模型MSE仅为$\frac{v}{k}$。这意味着集成MSE的期望会随着集成规模增大而线性减小。换言之,ensemble model至少与它的任何成员表现得一样好,并且如果成员的误差是独立的,ensemble将显著地比其他成员表现得更好。
NN能找到足够多的不同解,意味着它们可以从Model Averaging中受益(即使所有模型都在同一个数据集上训练))。NN中随机初始化的差异、不同输出的非确定性往往足以使得ensemble中的不同成员具有部分独立的误差。
Dropout
Dropout可以被认为是集成大量DNN的实用Bagging。Dropout训练的ensemble包括所有从base NN除去非输出单元后形成的子网络。
Dropout训练与Bagging训练不太一样,Bagging中所有模型都是独立的,在Dropout中所有模型共享参数。其中每个模型继承父神经网络参数的不同子集。参数共享使得在有限可用的内存下表示指数级数量的模型变得可能。
若使用0.5的keep_prob,权重比例规则一般相当于在训练结束后将权重除以2,然后像平常一样使用模型。实现相同结果的另一种方法是在训练期间将单元的状态乘以2。
Dropout是一个Regularization技术,它减少了模型的有效容量,为了抵消这种影响,我们必须增大模型规模。当Dropout用于Linear Regression时,相当于每个输入特征具有不同weight decay系数的$L_2$ weight decay。每个特征的weight decay系数的大小是由其方差来确定的。其他Linear Model也有类似的结果。对于Deep Model而言,Dropout与weight decay是不等同的。
Dropout是一种非常有效的防止过拟合方法,它可以被理解为是在训练阶段,将神经网络中的一些结点及其连接按一定的概率$p$($p$通常设置为0.5或0.7)进行删减,可看作是许多子网络的Bagging。需要注意的是神经元结点的以概率$p$随机擦除只发生在训练阶段,在测试阶段,我们保留所有的神经元结点,但是需要对权重$w$乘以dropout概率$p$,即$\hat{w}\leftarrow w\times p$。这样可以保证任何隐层结点输出的期望和可以和实际输出保持一致。对原网络施加dropout等同于从原网络采样多个子网络,一个拥有$n$个结点的神经网络,可得到$2^n$个子网络结构。和Bagging不同的是,这些子网络的权重都是共享的,因此所有的参数量依然是$O(n^2)$。
Dropout的idea来自于生物进化理论:孩子需要从其父亲和母亲分别继承一般的基因,来让自己的生长、以及应对环境方面更加robust。那既然大自然都是这么做的,作者当然也将这个idea用在了Deep Learning里面。加了dropout之后,可以减少DNN中每个neuron对其他neuron的依赖,从而可以让自己学习到更加robust and discriminative的feature,哪怕其他neuron挂了(被dropout掉了)我也依然能让网络work。
Dropout还可以被理解为向网络的hidden layer施加noise来作为regularization。
以一个具备$L$个隐层的神经网络为例,另$l\in \{1,\cdots,L\}$代表第$l$个隐层,$z^{(l)}$代表第$l$个隐层的输入,$y^{(l)}$代表第$l$层的输出($y^{(0)}=x$为输入),$W^{(l)}$和$b^{(l)}$分别代表第$l$层的权重和偏置,$f$代表非线性变换函数。未施加dropout时,网络的前向计算如下:
$$
z^{(l+1)}_i=w^{(l+1)}_i y^l + b^{(l+1)}_i
$$
$$
y^{(l+1)}_i = f(z^{(l+1)}_i)
$$
施加dropout后,网络的前向计算如下:
$$
r_j^{(l)}\sim Bernoulli(p)
$$
$$
\tilde{y}^{(l)} = r^{(l)}\ast y^{(l)}
$$
$$
z^{(l+1)}_i=w^{(l+1)}_i \tilde{y}^l + b^{(l+1)}_i
$$
$$
y^{(l+1)}_i = f(z^{(l+1)}_i)
$$
其中,$\ast$代表点乘运算,$r^{(l)}$代表相互独立的Bernoulli随机向量,其每一维值为1的概率是$p$。
DropConnect 是Dropout的一个特殊情况,其中一个标量权重和单个hidden unit状态之间的每个乘积被认为是可以丢弃的一个单元。
Batch Normalization 在训练时向hidden unit引入加性和乘性噪声重新参数化模型。BatchNorm主要目的是改善优化,但噪声具有正则化效果,有时没必要再使用Dropout。
Adverserial Training
DNN对对抗样本非常不robust的主要原因之一是 过度线性。DNN主要是基于线性块构建的,因此在一些实验中,它们实现的整体函数被证明是高度线性的。这些线性函数很容易优化,不幸的是,如果一个线性函数具有许多输入,那么它的值可以非常迅速地改变。如果我们用$\epsilon$改变每个输入,那么权重为$w$的线性函数可以改变$\epsilon||w||_1$之多,如果$w$是高维的这会是一个非常大的数。Adverserial training通过鼓励网络在训练数据附近的局部区域恒定来限制这一高度敏感的局部线性行为。这可以看作一种明确地向监督NN引入局部恒定先验的方法。
对抗样本也提供了一种实现semi-supervised learning的方法,在与数据集中的label不相关联的点$x$处,模型本身为其分配一些label $\hat{y}$。模型的label $\hat{y}$ 未必是真正的label,但如果模型是高品质的,那么$\hat{y}$提供正确标签的可能性很大。我们可以搜索一个对抗样本$x^{‘}$,导致分类器输出一个标签$y^{‘}$且$y^{‘}\neq y$。不使用真正的label,而是由训练好的model提供label产生的adverserial samples被称为“虚拟对抗样本”。我们可以训练分类器为$x$和$x^{‘}$分配相同的标签。这鼓励classifier学习一个沿着未标注数据所在流形上任意微小变化都很robust的函数。驱动这种方法的假设是,不同的类通常位于分离的流形上,并且小扰动不会使数据点从一个类的流形跳到另一个类的流形上。
DropBlock
Paper: DropBlock: A regularization method for convolutional networks
熟悉Dropout的同学们可能都知道,它是一种非常有效的正则化方法,并且通常用在fully connected layers,但是在conv layers却不那么work了。而造成这种现象的原因就在于dropout是随机drop掉一些feature的,而conv layers中的activation units是spatially correlated的,所以即使你加了dropout,信息依然可以在不同conv layers之间流动,而没法儿完全解耦。本文提出的DropBlock就是来弥补dropout的这个缺陷的。
这是一篇发表在NIPS’18上的paper,idea其实非常非常简单,下面就来进行一下简要的梳理吧。
DropBlock,顾名思义,就是将feature map中的一块连续区域一起drop掉。因为DropBlock丢掉了correlated area的feature,所以使得网络不得不去其他area寻找合适的activation units来拟合数据。
注:这部分的也可从生物进化的角度理解,和上面的dropout类似,读者可参考上面对dropout的讲解一起阅读,此处不再赘述。
结合下图解释一下吧: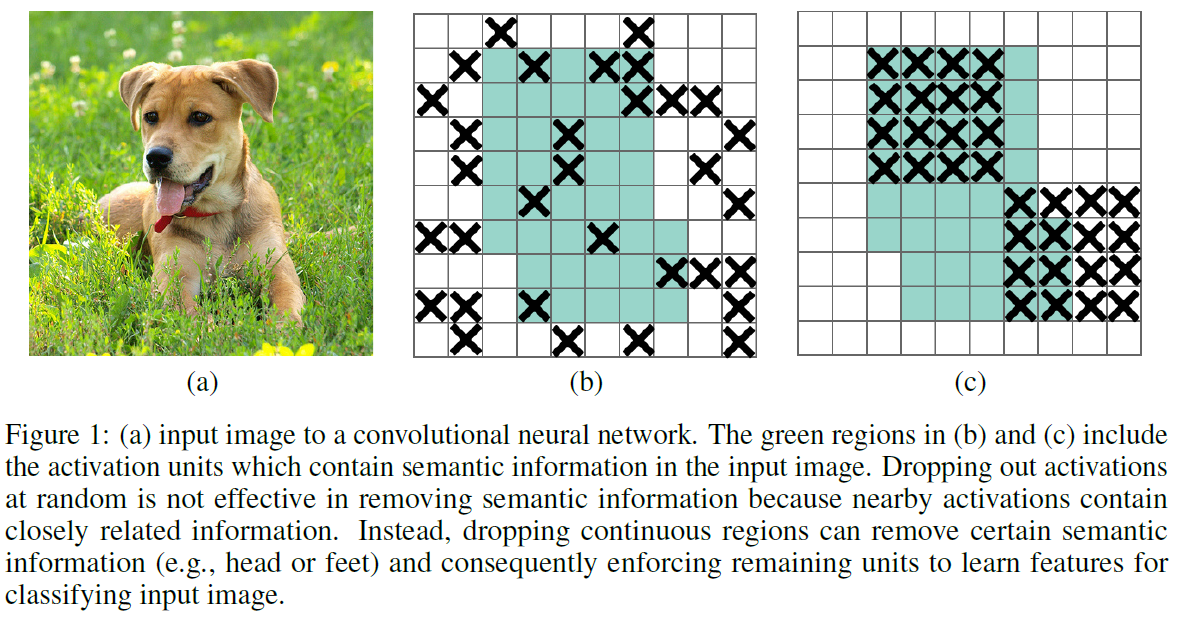
图中蓝绿色区域代表image中包含semantic meaning最多的region,(b)是随机drop掉一些activation units,而随机drop掉activation units的方式不够effective,因为相邻的activation包含closely related information;(c)是DropBlock,即drop掉一块连续的semantic region,这样可以迫使网络中剩余的units学习到更好的feature来准确分类。
作者在实验中发现使用DropBlock的正确姿势如下:在训练的初始阶段,先使用比较小的DropBlock ratio,然后线性增大DropBlock ratio。
DropBlock有两个超参:$block_{size}$和$\gamma$,其中$block_{size}$就是feature map中被drop掉的大小,$\gamma$代表被drop掉的activation units的数量。
DropBlock的算法细节如下: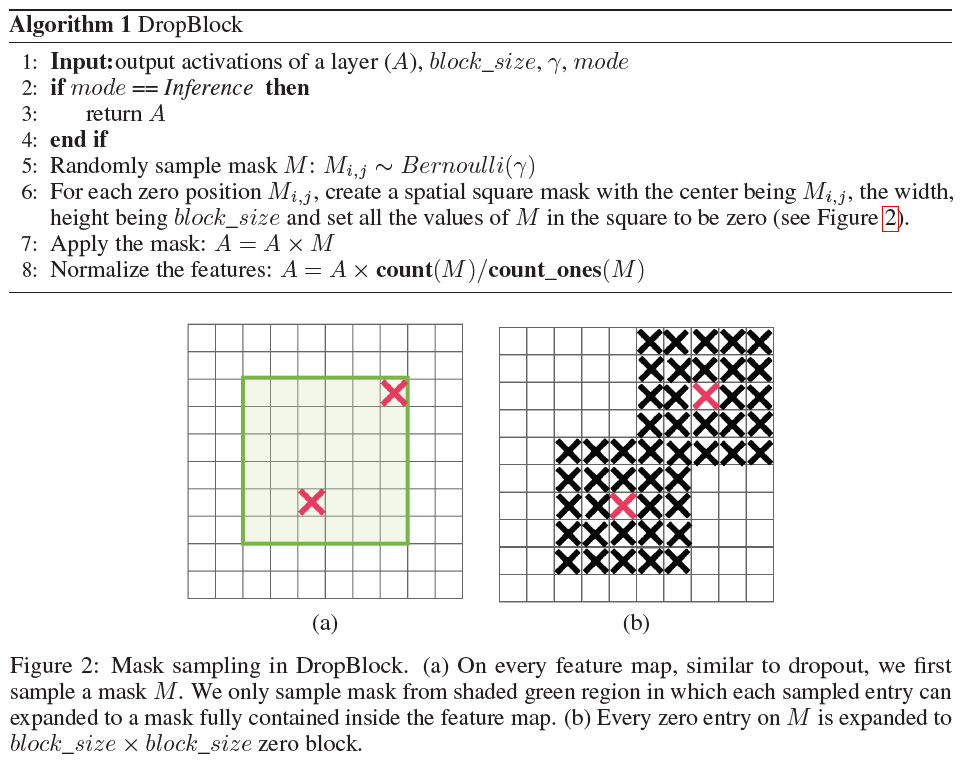
和dropout一样,DropBlock也只在training阶段使用,不在inference的时候使用。DropBlock同样可以理解为exponentially-sized小网络的ensemble。These sub-networks
include a special subset of sub-networks covered by dropout where each network does not see contiguous parts of feature maps.
关于调整超参:
- 当$block_{size}=1$时,DropBlock就和dropout一样,当$block_{size}$ cover到整个feature map时,就和另外一种regularization方法SpatialDropout一样了。
- 在实际中,其实并不需要显示地指定$\gamma$的值,$\gamma$可通过如下方式计算:
$$
\gamma=\frac{1-keep_{prob}}{block_{size}^2}\times \frac{feat_{size}^2}{feat_{size}-block_{size}+1}
$$
下图是CAM可视化的结果: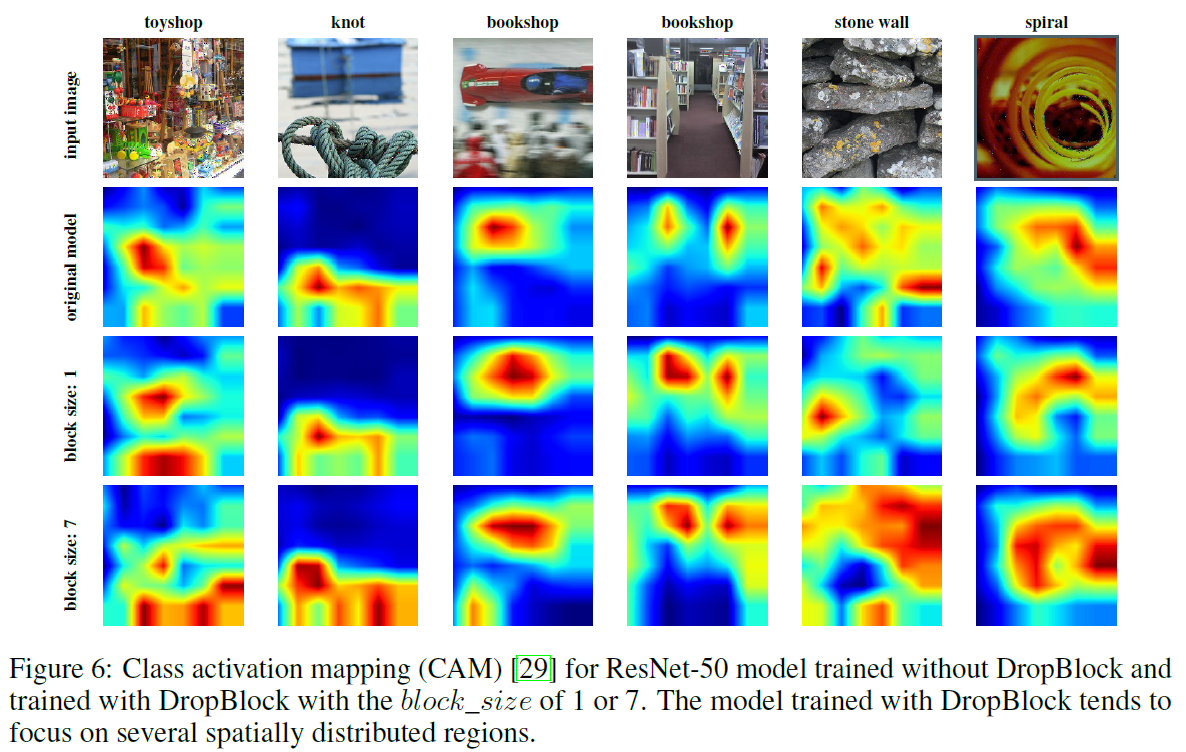
可以明显看出,用了DropBlock的网络学习到了spatially distributed representations。而且用了更大的block_size后的模型代表更强的regularization,因此模型效果也越好。
此外,在detection的实验中,作者发现train from scratch的RetinaNet效果比fine-tune from ImageNet的要好,而且加了DropBlock之后的RetinaNet能带来更大的提升,这说明DropBlock对于object detection是一种非常有效的regularization方法。
Reference
- Goodfellow, Ian, Yoshua Bengio, and Aaron Courville. Deep learning. MIT press, 2016.
- Srivastava, Nitish, et al. “Dropout: a simple way to prevent neural networks from overfitting.” The Journal of Machine Learning Research 15.1 (2014): 1929-1958.
- Ghiasi, Golnaz, Tsung-Yi Lin, and Quoc V. Le. “DropBlock: A regularization method for convolutional networks.” Advances in Neural Information Processing Systems. 2018.
