[DL] Batch Normalization

2018-11-20 PV:

Introduction

Batch Normalization是现如今主流深度学习模型必备组件。笔者认为，这是一个和ResNet里提出的skip connection一样对深度学习发展十分insightful的idea。本文旨在对BatchNorm进行一下系统的梳理与讲解。

Paper: Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift

训练Deep Models通常是比较麻烦的，以feedforward network为例，每一层输入distribution的改动都会影响其后继的层，若使用了Sigmoid这样的non-linearity transformation，则还会存在saturation的问题(sigmoid两端)。

BatchNorm通过对每一个mini-batch samples做normalization，可以极大地减小这种internal covariate shift，从而让整个网络使用更大的learning rate，取消因防止overfitting对Dropout的依赖，不需要可以关注param initialization等。

假设DNN的optimization object如下：
$$
\Theta=\mathop{argmin} \limits_{\Theta} \frac{1}{N} \sum_{i=1}^N l(x_i, \Theta)
$$

使用SGD优化算法的话，会随机sample一个mini-batch，使用mini-batch而非one-by-one的好处在于：

一个batch的gradient是对整个training set中的estimation，若batch size越大显然就会得到更准确的estimation
计算一个mini-batch的gradient显然比one-by-one sample更为高效

SGD虽然有效，但是在feedforward network的训练中会存在一些问题，例如某一层的input会受到其前驱层的影响，所以在DNN中一个小的扰动都会对整个网络的训练带来很大的影响。

若一个learning system的input发生了变化，我们就称该system经历了covariate shift。

BatchNorm通过对input进行normalization来减小这种internal covariate shift，此外，BatchNorm通过减少gradient对参数初始化和网络模型参数量的依赖，也会利于gradient flow，在DNN中加入BN层后，允许我们使用更大的learning rate，以及sigmoid activation function (不用担心两端的saturation问题)。此外BatchNorm还有正则化的作用(引入了加性和乘性噪声)，从而减少了防止overfitting背景下对Dropout的依赖。

Normalization via Mini-Batch Statistics

对于每一层的input：$\hat{x}^{(k)}=\frac{x^{(k)}-E[x^{(k)}]}{\sqrt{Var[x^{(k)}]}}$
其中，$E[x^{(k)}]$和$Var[x^{(k)}]$从整个training set上计算而来。

但是单纯只做normalization会改变layer的表示能力，因此还需要scale and shift the normalized value，也就是这样的：
$$
y^{(k)}=\gamma^{(k)}\hat{x}^{(k)} + \beta^{(k)}
$$
其中，$\gamma^{(k)}=\sqrt{Var(x^{(k)})}$，$\beta^{(k)}=E[x^{(k)}]$。

BatchNorm Transform

每个normalized activation $\hat{x}^{(k)}$可以视为线性变换$y^{(k)}=\gamma^{(k)}\hat{x}^{(k)} + \beta^{(k)}$后子网络的输入。

BN层的参数更新过程如下：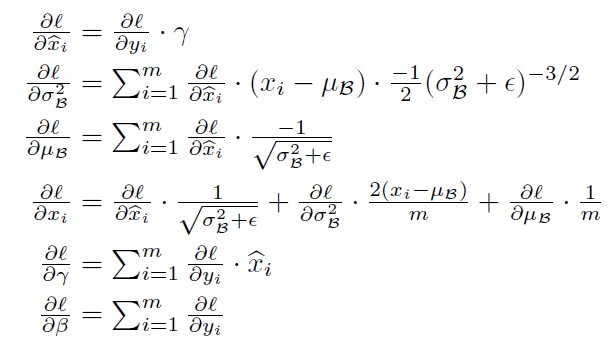
Update of BN Layer

BN层的训练过程如下：
Training of BN Layer

BatchNorm in CNN

BN在CNN中和MLP中有一些差别，CNN中，BatchNorm Transform独立地应用到每一维的channel$x=Wu$上，每一个channel对应的学习参数$\gamma^{(k)}$和$\beta^{(k)}$。

Batch Normalization enables higher learning rates

通过对activations进行归一化，可以避免在DNN中小的数据扰动对整个网络的影响。此外，BN也使得训练过程对parameters scale更加适应，当learning rate过高，在DNN的BP中，很容易出现gradient explosion和divergence。但是，添加了BN层后，BP就不受parameters scale的影响了。
例如：
$$
BN(Wu)=BN((aW)u)
$$
BP时：$\frac{\partial BN((aW)u)}{\partial u}=\frac{\partial BN(Wu)}{\partial u}$。此外，$\frac{\partial BN((aW)u)}{\partial aW}=\frac{1}{a}\cdot \frac{\partial BN(Wu)}{\partial W}$，所以larger weights会导致smaller gradients。

Reference

Ioffe S, Szegedy C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift[C]//International Conference on Machine Learning. 2015: 448-456.