[DL] BackPropogation

2018-07-25 PV:

Introduction

反向传播是神经网络训练过程中非常重要的步骤。目前许多深度学习框架以（例如Tensorflow）已在定义的computational graph中自行帮开发者完成了反向传播算法的计算。但是作为深度学习领域的研究人员，还是应该了解该算法的本质。本文就对该算法进行深入讲解（素材来自Stanford CS231n Spring,2017）：
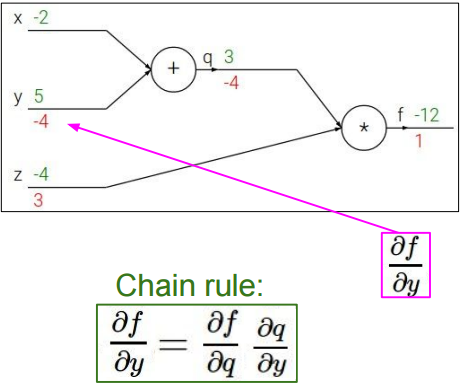
一个简单的computational graph $f(x, y, z)=(x + y)z$ (e.g. $x = -2$, $y = 5$, $z = -4$)是这样的：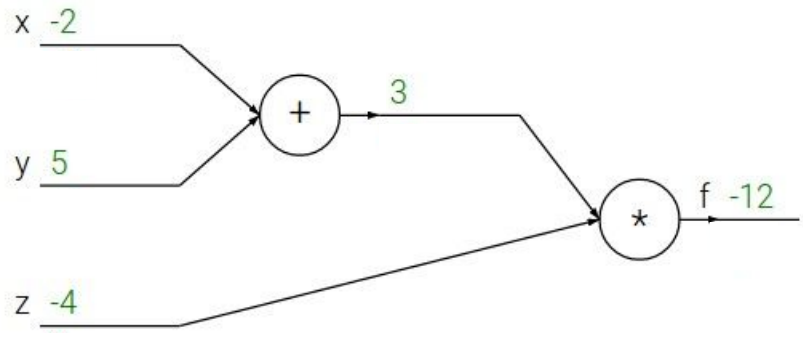
Fig. 1

令$q=x+y$，则$\frac{\partial q}{\partial x}=1,\frac{\partial q}{\partial y}=1$

可得$f=qz$，则$\frac{\partial f}{\partial q}=z=-4, \frac{\partial f}{\partial z}=q=3$

Fig. 2

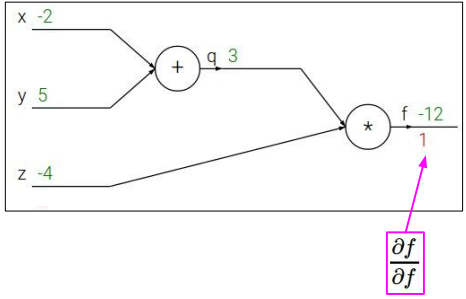
同时，$\frac{\partial f}{\partial f}=1$

Fig. 3

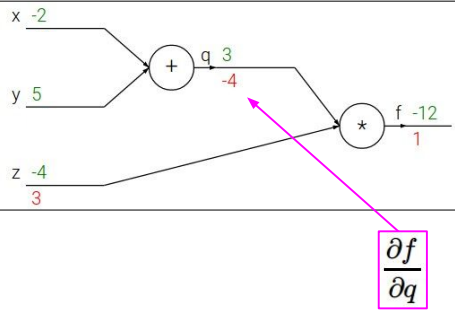
由链式法则可得：

$\frac{\partial f}{\partial x}=\frac{\partial f}{\partial q}\frac{\partial q}{\partial x}=-4$

$\frac{\partial f}{\partial y}=\frac{\partial f}{\partial q}\frac{\partial q}{\partial y}=-4$

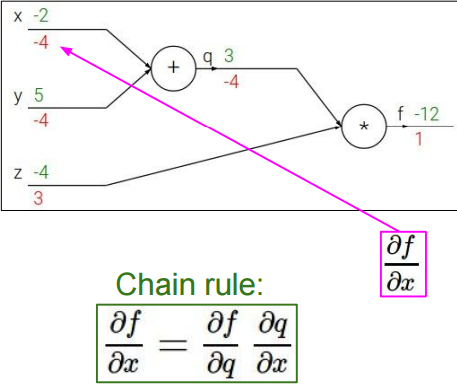
Fig. 4.1

Fig. 4.2

至此，对于反向传播算法的初步介绍就结束了，下面我们再来看一个更深入的例子：

定义computational graph：
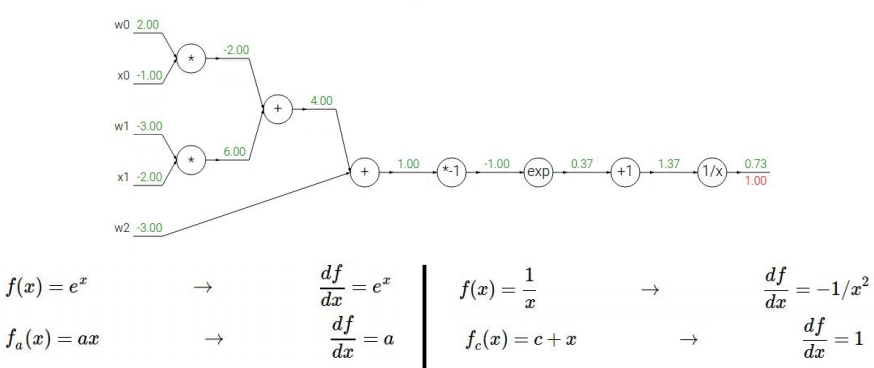
$f(w,x)=\frac{1}{1+e^{-(w_0 x_0+w_1 x_1+w_2)}}$

同样地，第一步反传，先求$\frac{\partial f}{\partial f}=1$；再求$\frac{1}{x}$(将分母视为大的变量x)的导数：

Fig. 5

Fig. 6

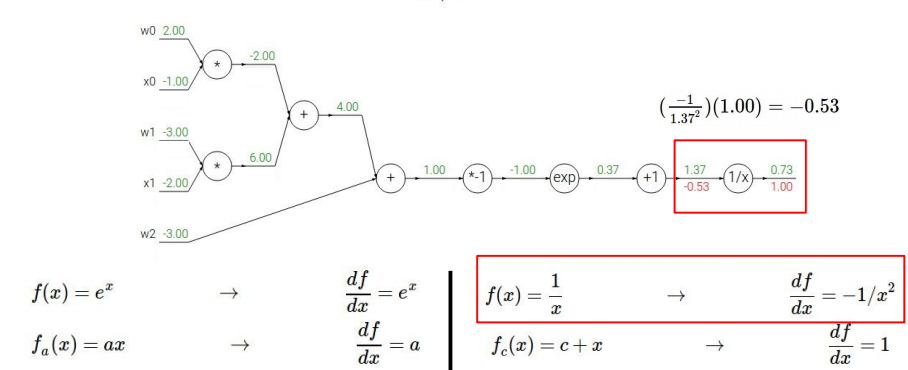
接下来求1+x(将分母的指数函数一块视为一个整体变量x)的导数：

Fig. 7

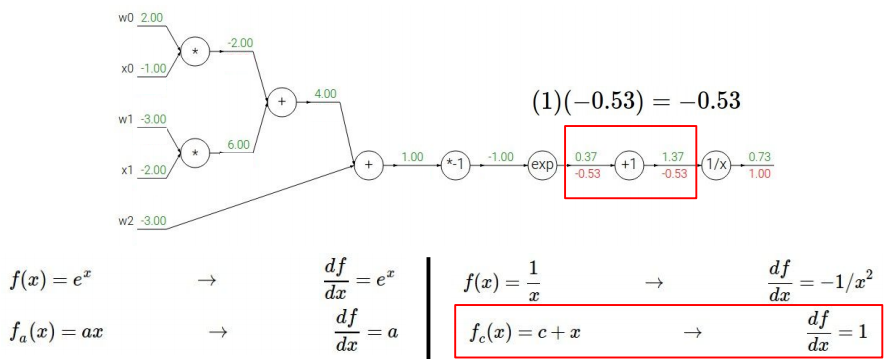
现在求分母里大的指数函数的导数：

Fig. 8

Fig. 9

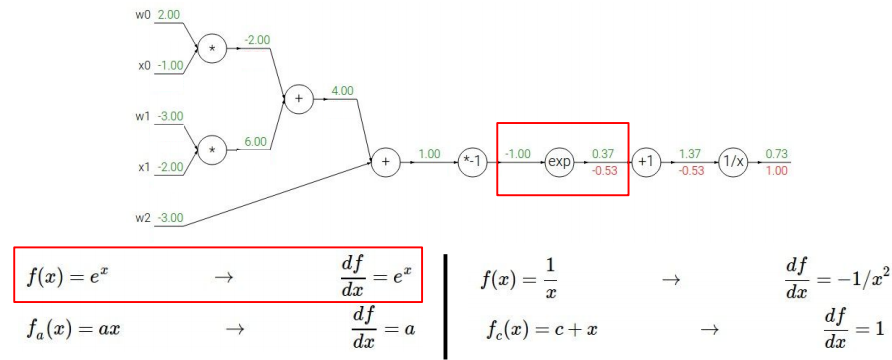
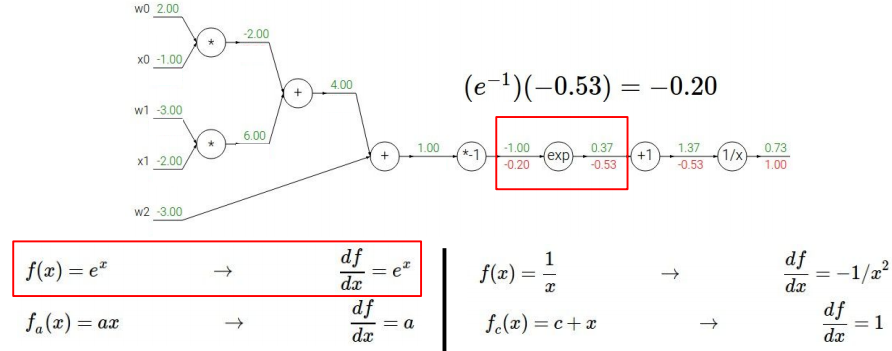
注意这里的处理方式：将$-(w_0 x_0+w_1 x_1+w_2)$视为一个整体。$e^{-1}$的来源是因为$-(w_0 x_0+w_1 x_1+w_2)=-1$。

接下来再处理$-x$(将$w_0 x_0+w_1 x_1+w_2$视为整体变量$x$)，显然易得：

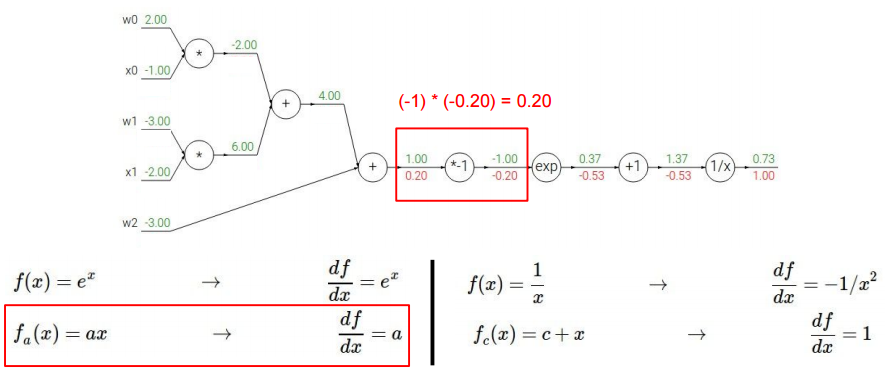
Fig. 10

接下来处理$w_0 x_0+w_1 x_1+w_2$(公式1)，公式1对$w_2$求导结果为1，再乘以之前反向计算的梯度$1×0.2=0.2$。公式1对$X=w_0 x_0+w_1 x_1$求导结果为1，再乘以之前反向计算的梯度$1×0.2=0.2$。

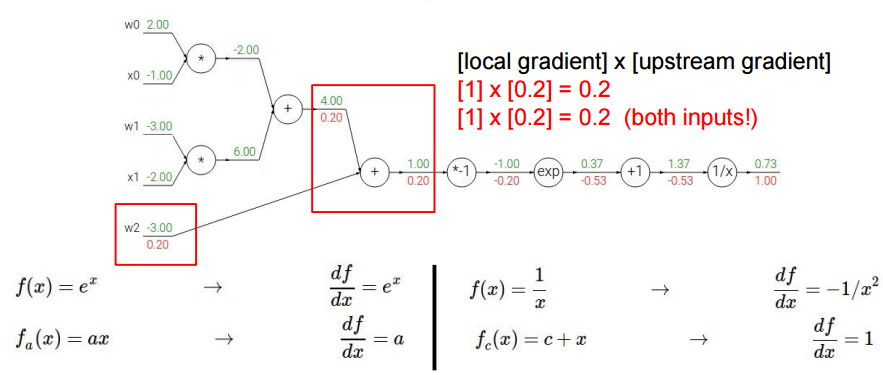
Fig. 11

接下来处理$w_0 x_0+w_1 x_1$，易得：

Fig. 12

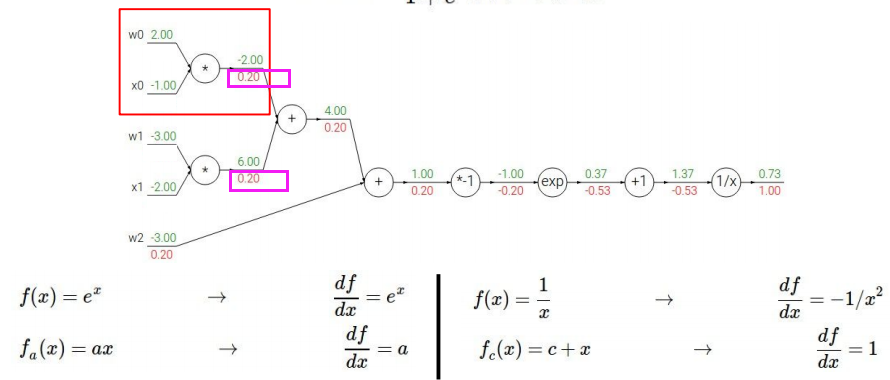
接下来处理$w_0 x_0$和$w_1 x_1$

Fig. 13

例子中的激活函数选用的是Sigmoid函数，利用Sigmoid函数的性质$\frac{d\sigma_x}{dx}=(1-\sigma(x))\sigma(x)$可得：

Reference